|
THEHISTORY OF MUSIC LIBRARY |
THE HISTORY OF MUSIC (art and Science)FROM THE EARLIEST RECORDS TO THE FALL OF THE ROMAN EMPIRE.
CHAPTER I. THE EGYPTIANS.
The most convenient basis for a history of ancient
music seems to be the early Greek system, for we are here removed from the land
of myths, and have the foundation upon which the superstructure of modem art
has been raised. The discoveries that have been made in Egypt and in Babylon,
within the century that has now passed, since Sir John Hawkins and Dr. Burney
wrote their Histories of Music, have revealed an advanced state of the art in
most ancient times, which was before unknown and unsuspected. There is no
longer room to doubt that the entire Greek system was mainly derived from
Egypt, Phoenicia, Babylon, or other countries of more ancient civilization than
Greece. The musical instruments of the Greeks may be traced in Egypt, even to
the hitherto unobserved Magadis, or Octave playing
instrument, of Anacreon, and to the little wailing long pipe used for
lamentations on the death of Adonis. From that pipe must the modern hautboy
claim its descent. The total number of notes in the combined Greek scales agrees
precisely with the enumeration of the Egyptian system, as revealed to us by
Greek writers. The worship of Athena, or Minerva, who corresponds to the
Egyptian goddess Neth, was attended by the peculiar custom of having musical
instruments to play in Octaves in the temples of both countries. The same
system of music must have prevailed in the two, because they had, at least in
one case, the same song, and it was a song that, according to Herodotus, was in
general use.
Moreover, a further discovery may be noted through
Egyptian monuments, that, at the time of the building of the Pyramids, and
before the invasion of the Hyksos, or Shepherd Kings, had made every shepherd
an abomination to the Egyptians, those Egyptians had bands that played with
harps and pipes, in concert, not in unison, as might have been supposed, but in
harmony. This is made manifest by at least one of the representations on the
tombs of the fourth dynasty of Egypt.
Another point worthy of observation is the practical
agreement and general identity between the musical instruments of Egypt and
those of Nineveh and of Babylon. This is largely exhibited in ancient
sculptures, and may be observed by any visitor to the British Museum. If we
couple with this resemblance the incidental notice of the Chaldean division of
the Octave, by Plutarch, and that of the reputed Diatessaron, or
musical interval of a Fourth, in the Babylonian planetary system, by Dion Cassius,
they should suffice to establish the identity of the musical systems of Assyria
and Egypt.
When examined by this new light, the musical
acquirements of the Greeks will appear but as one branch of the transfer of
learning from Asia to Europe; for the Egyptians were admittedly of Asiatic
origin. It will also raise doubts as to many of the inventions that were
posthumously attributed to Terpander, to Pythagoras, and to other Greeks.
Lastly, perhaps the most interesting feature of all
will be to establish, that the notes of the scale in this dark backward and
abysm of time, differed in no other way from modern notes of the minor scale
(as on the long keys of a pianoforte, beginning on A), than in the manner of
tuning the intervals called Thirds, (as from A to C and C to E,) so that,
although falling short of being consonant, as ours are, they would pass for
Thirds in melody, and not every ear would perhaps then detect the difference,
since it was but the eighty-first part of a string. If, after this, the ancient
technicalities can but be successfully cleared away, the reader may have the
whole subject of this most ancient music before his mind's eye. This will be
here attempted.
Boeckh has remarked, in his Metres of Pindar,
that ‘the music of the ancients is not merely neglected by the students of
antiquity, but is buried in oblivion.’ It is now quite time that it should be
disinterred. It has indeed been allowed to remain an unravelled puzzle for many ages, and its complexities have seemed rather to increase than
to decrease with the onward progress of time. The reasons for this have been
various.
First, it presented a difficulty to the Romans because
they had adopted but one portion of the Greek system, and did not trouble
themselves over much about the remainder. Cicero thought that Aristoxenus had devoted his energies too exclusively to
music; and, when touching upon the art in his own writings, Cicero translated
from Aristotle, and then Quintilian copied from Cicero. Vitruvius had to travel
beyond the boundary of the Roman musical system when he wrote about the metal
vases that were constructed within theatres to echo sound, and so to give
resonance to the voices of the actors. He then described Greek musical
literature as ‘an obscure and difficult subject,’ and one that could not be
explained without resorting to Greek words, for which there were no Latin
equivalents. Although he endeavoured to understand
and to explain the writings of Aristoxenus, he did
not always succeed in giving correct interpretations of his author.
Many such imperfect renderings might be cited from
Roman authors, but it will now suffice to pass on to two of the latest writers
under the old empire. Their works exercised the greatest influence upon the
music of the middle ages. These were Cassiodorus and Boethius, who were
cotemporaries in the sixth century, in the reign of Theodoric, the Ostrogoth.
Cassiodorus was a Christian who wrote upon the liberal
arts generally, and devoted but a part of his treatise to music. He included
only the branch of Greek music that had been adopted by the Romans, viz., the
ordinary Diatonic scale of tones and semitones, like our own, but in its early
Pythagorean, or unimproved, state. His treatise is, so far, a good and brief
summary, and it includes the ratios of the simple consonances, such as the
Fourth, the Fifth, and the Octave. But when he touches upon compound intervals,
it is not good For instance, he says, or has been made to say, that an
Eleventh, (i.e., a Fourth added to an Octave,) is a consonance, and that
it is in the ratio of 24 to 8a (which would be as 3 to 1), whereas it is
not a consonance, and is not in the ratio of 24 to 8, but of 8 to 3. To treat
an Eleventh as a consonance was a common error, for which he had respectable
authority, but not for mistaking its ratio.
The work of Boethius (De Institutione Musica) is the most elaborate of the Roman treatises, and one devoted
exclusively to music. It is divided into five books, each subdivided into some
twenty or thirty heads, or chapters. The last book exists only in an imperfect
state. Boethius seems to have intended it to consist of thirty chapters, of
which but eighteen are extant. The index of contents shows that the last twelve
were to have been devoted to a summary of the suggestions and improvements of
the later Greek writers, and especially to those of Claudius Ptolemy. But the
summary was to have been historical only, because he had already formed his
calculations of musical intervals upon the antiquated system of the Pythagorean
scale. That was the adopted scale of the Romans, and his calculations upon it
had been embodied in the preceding books of his treatise.
Boethius, in contrast to Cassiodorus, seems to have
paid more attention to the science than to the art of music. He was an able
arithmetician, but fell short of the attainments necessary for a great writer
upon the theory of music. Yet he exalted theory greatly above practice. His
acquaintance with the practical branch of his subject was evidently slight;
indeed, so slight that he seems not to have known the correct names for the
strings of the lyre. He applied the title of lichanos,
or fore-finger string, to two that have not that name in the work of any extant
Greek author, and they were strings which the Greeks intended for the plectrum.
The Romans had Latin designations for the strings long before the time of
Boethius, which may account for his imperfect acquaintance with the Greek
nomenclature
Boethius should be ranked rather as a man of general
learning than as a remarkable musician. He adopted Claudius Ptolemy’s theory,
that the combination of an Octave with a Fourth above it, is a consonance,
against which the Pythagoreans had systematically, and (as will be hereafter
clearly proved) had rightly contended. But still he had only read Claudius
Ptolemy’s works superficially, or else he would not have given currency to the
popular story of Pythagoras and the hammers that Pythagoras discovered the law of musical
consonances through passing a blacksmith’s shop, and weighing the hammers that
were striking Fourths, Fifths, and Octaves upon an anvil. Ptolemy denies the
possibility of such consonances from one anvil (in his third chapter of Book
I.), and even a little reflection might have taught Boethius that the tone of a
bell cannot be altered in pitch, by changing the weight of its clapper.
Boethius did not adopt the improvements either of
Didymus or of Ptolemy in the musical scale, but retained the old Pythagorean
system of major tones only, instead of alternating major and minor tones. Hence
all his intervals of Thirds (whether major or minor Thirds) were discords
instead of concords. Yet Didymus had shown the way to produce true consonant
major and minor Thirds, five hundred years before the date at which Boethius
was writing. Claudius Ptolemy had again demonstrated it, by inverting the succession
of tones, about a century, after Didymus, so that if Boethius had been a sound
theorist or a practical musician, he could not have failed to discover, in the
one case by the Pythagorean law of consonances, and, in the other, by his ears,
how great was the improvement of turning those discords into concords, and, at
the same time, improving the proportions of the so-called semitone.
Again, if Boethius had been well versed in the history
of Greek music, he would not have handed down a series of stories that this
man, and that man, added a new string to the lyre as if it were to be
understood in a literal sense. He would have discovered the chronological (as
well as other) contradictions which such claims involved, and that adding a new
string to the lyre could but be an ancient idiom for having introduced some
approved novelty into the arts of poetry and music.
For these various reasons Boethius does not merit so
high a rank among ancient writers on music as has been conceded to him in
England, by making his treatise the text-book in our Universities.
No Roman of antiquity is known to have made, or even
to have attempted, any improvement in the science of music. The Romans received
the Diatonic Scale, of tones and semitones, from the Greeks at a time when it
existed only in its primitive and imperfect form. Nevertheless they were
content to retain it so, and did not follow the Greeks in any subsequent
improvement. It is for that reason Greek music cannot be effectually learnt
from Roman writers.
The treatise of Boethius having been the most complete
that had been written in the Latin language, and being supposed to teach the
best system, was unfortunately adopted as the text-book in the middle ages. It
had a very retrograde effect upon music, one of the evils being, that it kept
up the use of an antiquated and ill-divided scale to the time of Guido d’Arezzo, who taught and revived it in the eleventh
century.
In after ages Boethius, in some way, gained the repute
of having been a Christian philosopher. This may have been, because his system
of music had been adopted in the Church. It is possible, also, that he may have
been mistaken for another person of that not uncommon name, for no one could
have written upon music less in the manner of a Christian than the author of
the Institutio Musica.
In a treatise on music of early date, a man could but
with difficulty avoid giving an indication of his religious creed, and a
Christian especially would almost surely make some sign of his belief, unless
he had a direct interest in avoiding it. There was no motive like that of a
general persecution to induce concealment at the time Boethius wrote, so that,
if any one should now be curious as to the religion of that able writer, he may
perhaps satisfy himself that there is not a symptom of Christianity about his
writings on music. The contrast of style will be apparent on comparing a few of
the corresponding pages in the treatises of the two cotemporaries, Cassiodorus
the Christian, and Boethius the philosopher of questionable creed.
A second element of confusion to the student of Greek
music arose from the employment of Greek words in ecclesiastical music, where
they were applied in senses sometimes opposite, and at other times differing
materially from classical Greek. As one instance, the alternate singing of
verses of psalms by a choir divided into two parts, was introduced from Antioch
in the fourth century. One half of the choir sang one verse, or part of a
verse, and the other half responded, either with the next verse, or with a
burden, such as, For His mercy endureth for ever, in Psalm No. 136; much like the present
practice in our cathedrals. It was a Syrian and a Jewish manner of responsive
singing. The Song of Triumph of Deborah and Barak (Judges, chap. v.), and
Psalms, such as Nos. 103 and 104, were evidently designed for it; but it was
not before practised by the Greeks, or else it would
not have been a novelty. Yet a Greek term was soon appropriated for it, but in
quite a new sense. It was called antiphonal singing; but the meaning of
the Greek anti, as usually applied to music, is in the sense of accompanying,
and, therefore, in that of the Latin cum, with, and not of pro,
or contra. Instead of being responsive, like the chants in our cathedrals
(which in Greek would be called ameibomenai),
Greek antiphons were simultaneous sounds an Octave apart; and therefore like
our congregational singing, wherein the voices of men intermingle with those of
women and children. The voices of the men, being naturally an Octave lower than
the others, make the antiphons. Thus, Greek antiphona were
fellow or companion sounds, harmonious and concordant. The graver of the two
notes of the Octave, says Aristotle, is the antiphon and concordance to the
upper; they result from young boys and men singing together. (Some of the
latest writers include double Octaves as antiphons.) Aristotle says that,
although Fourths and Fifths are also consonances, yet they are never sung in
sequences to make antiphona, as are Octaves. In
this respect Greek ears agreed with our own. Ample definitions are found in the
works of Plato, of Aristotle (many), of Plutarch, and his cotemporary
Theon of Smyrna, of Gaudentius, of Psellus, in the
eleventh century, and of Bryennius, in the
fourteenth, thus carrying down the classical meaning of the
word antiphon to the Byzantine-Greek, in the time of the Emperor
Palaeologus the elder, about 1320.
As the translations of so many passages in classical
authors are affected by this anti, a few more cases should be cited before
passing from the subject. The oldest of our extant lexicons are not here to be
much defended upon. In that of Hesychius, antichorda are
first explained as companion strings, which is right; but, secondly, as equal
strings, which is not right, according to classical authors. The second
definition was probably interpolated to agree with the meaning adopted in the
Western Church, for strings an Octave apart could not be equal. The
Greek antichorda were always Octave
strings, and pros-chorda were the equal strings, or unisons. They
are so explained by Plato, by Aristotle, and by Plutarch. When Plutarch states
that Archilochus was supposed to be the first person who played an
accompaniment on the lyre under the voice part, and that the ancients had
always before played in unison with it, he expresses the unison
strings by proschorda. Antiphthongus and antipsalmus are
two other words that equally express simultaneous (Octave) sounds. The first is
used as a synonyme for antiphon, by Pindar, as
quoted by Athenaeus. Again, antispasta mele,
and antispasta sunchordia,
quoted by him from Phrynichus, and from Sophocles, (both meaning Octave
accompaniment) and antitheton for antiphonon, by Aristotle.
Again, the antipsalmus must
necessarily have had the accompaniment of the hands upon a stringed instrument
to constitute a psalm, but Hesychius omits that part of the definition possibly
because stringed instruments were not in his time used in the Church.
The antistrophes of Greek plays are beyond
the scope of the present enquiry, but the musical part of the evidence seems to
run in the same direction. When Aristotle asks, Why are neither Hypo-Dorian nor
Hypo-Phrygian choruses sung in tragedies? Is it because they have
no Antistrophe? One sufficient musical reason for not having any would be,
that they were the two lowest base scales, and it was impossible for men to sing
Octaves below them. Whether that was or was not the reason, and whether
antistrophes were ordinarily sung in Octaves, or an Octave lower than strophes,
must be submitted to those who have studied the subject. Aristotle is good
authority for the lack of antistrophe to the two lowest base scales.
Octaves are the simplest form of consonance, and the
first step towards the power of appreciating other double sounds. Abundant
evidence may be found of the estimation in which this simplest and most perfect
of all harmony was held by the Greeks from very early date, and also by the
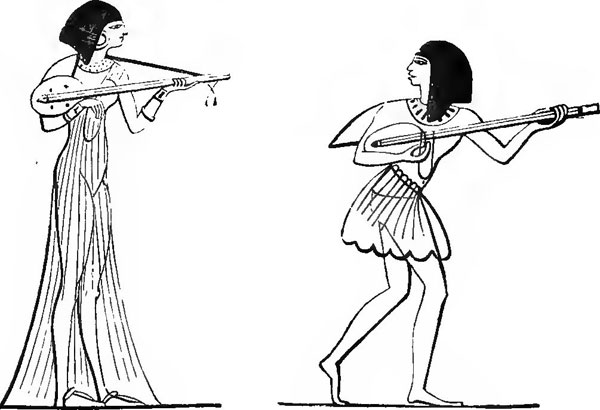
Egyptians before them. Anacreon, who is said to have flourished about 540 BC,
used to accompany his voice upon a ten-stringed instrument, in which each of
the strings was divided into two parts, so as virtually to make twenty, but ten
were tuned in Octaves to the others. That instrument was derived from Egypt;
but its ordinary compass, Egyptian or Greek, was of seven, instead of ten
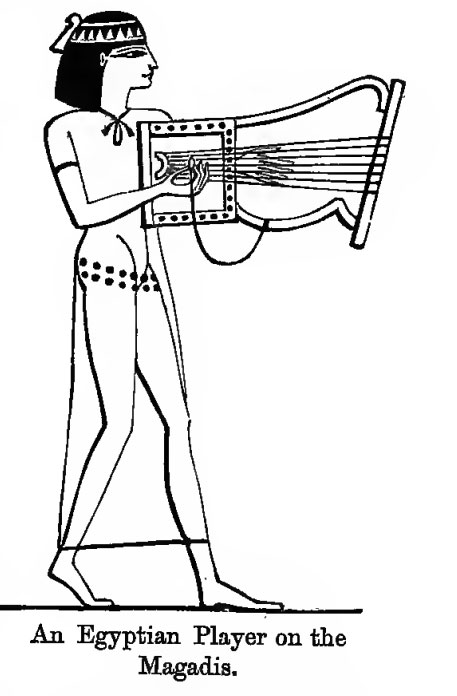
strings. The name, Magadis, may have been compounded
of magas, a bridge for a musical instrument,
and dis twice. The double bridge which divided each string into two
parts was at about a third of the sounding distance up the string, so as to
make one end double the length of the other; because half the length of any
equal sized string must sound an Octave above its whole length. This
instrument, which has hitherto been waiting for identification, will hereafter
be shown, both in its Egyptian and in its Greek form.
Long after the form of instrument used by Anacreon had
fallen into disuse (or was perhaps employed only in the worship of Athena), the
verb magadizein, to magadize,
was retained in the language to express playing in Octaves upon any
instrument whatever. Thus, even double pipes, that could have no bridges to entitle them to such a name, were called Magades,
if one of the pipes was tuned an Octave below the other.
The words that relate to music, in modern languages,
are mostly derived from the Greek, and yet there is scarcely one among them
(even one of commonest use) that retains its original meaning. The prime cause
of these deviations is our indirect inheritance of such words. We owe them
mainly to their having been appropriated for early Church music, and there was
a mediaeval taste for giving Greek names to everything musical, even though as
misapplied as in the case of antiphon. If the words were then received in their
new sense, it would matter little what ancient Greeks might have said to them.
In order to exemplify the deviations that thus arose,
and the trouble they have given to after-enquirers, a few of the most ordinary
words will be now cited.
The Greek Harmonia is quite a different
thing from modern harmony, whether in its French, Italian, Spanish, or
English sense; neither is it a synonyme for our melody,
as many learned men have supposed, including Dr. Franz, of Berlin, and Dr.
Burney, who followed Mason’s definition. It will be here proved to mean “The
System of Music”, or briefly Music, of which melody and harmony are each but
parts. For a short time the Enharmonic scale was so much in favour (owing to the popularity of the omission of Fourth and Seventh in a scale),
that scarcely any other than enharmonic was used, and so, for awhile, the teachers of that system assumed the general
name, applicable alike to all. Aristoxenus comments
upon this usurpation. But their system soon dropped out of favour,
and not long after, out of use. Again, Melodia is not at all the
equivalent to our melody, nor had Greek music given birth to what we
should consider melody, at the time the word was first used.
Greek Melos had not necessarily any tune in it. It applied to the
rising and falling sounds of the voice when linked together in speech, or in
rhythm, as well as in music; so that recitation, without any musical intervals
in it, would still be Melodia. Thirdly, Harmonike does
not mean harmonic, or harmonics, but is a synonyme for Harmonia. Again, Sumphonia does
not mean symphony. The last expresses our harmony, viz., concord of
notes of different pitch. Even music (Mousike)
in Greek had so extended a sense as to render necessary more precise words,
such as Harmonia, or Harmonike, to
express the more strictly musical parts of it. The mental training of a young
Greek was included in the word Mousike,
and it comprehended all that related to the sciences of sounds and numbers, as
well as to their application in practice.
A fourth element of difficulty for the student of
Greek music was in the ecclesiastical scales. They are not of the early date
that has been supposed; and, although they differed essentially from Greek
scales, they were called Greek, and had Greek names given to them. The origin
of Church music will require a chapter, which it is unnecessary to anticipate,
but it may be observed Here that Church writers condemned all music which
was not constructed upon the ecclesiastical system as false. They asserted their
own to be the only true ancient music. For this they had the authority of
Popes, such as John XXII, who declared all systems that differed from the
ecclesiastical to be frivolous novelties. It was safer in those days to be
orthodox, than to exercise private judgment against the traditions of the
Church. Ecclesiastical courts had wide jurisdiction, and very sharp claws.
Such a series of misleading elements will sufficiently
account for the ill-success of many learned men who tried to discover what
Greek music really was. It would hardly be suspected that the meaning of
ordinary words, which everyone is supposed to know, must first be rejected.
Therein lay the difficulty of translating many passages relating to music in
the works of classical authors. Latin translations are of no use, because the
Greek words are varied only as to their terminations. Such translations were easy
enough to make, because they did not demand that the translator should
understand his subject. There remains, also, sufficient evidence that advantage
was taken of that license.
As if there were not already a sufficient number of
intricacies in the pathway to Greek music, a glance at the works of some of the
late German historians shows that they have imported into it a new element of
complication. Beginning the study, as some may think, at the wrong end, they
would first settle which of the modern notes will most faithfully represent the
supposed ancient Greek pitch. That in itself is but a speculation, for thereare no certain grounds to go upon; but when historians
follow it up by altering the names of the Greek scales to correspond with modern
ideas of pitch, they dissever those scales from all their historical
associations. If we look into the work of a modern German author for the
Hypo-Dorian or Common Greek scale, it is no longer to be identified with
the Natural scale, the scala dura, (as on the
long keys of the organ or pianoforte, beginning on A,) as it used to be, and
still is with us. The Germans have changed it to one beginning on A flat, or on
some other note. Thus the important historical link between the ancient Common scale, and the modern Natural scale has been set aside. Secondly, the
basis of Plain Song, or Gregorian music, rests upon the combination of
the Greek Dorian and Hypo-Dorian scales, (D minor and A minor) but that is
also rendered unintelligible, and seems even to be contradicted by the
alteration, from A and D, to A flat and D flat. Thirdly, the long keys of the
pianoforte were inherited from, and still identify, the Common Greek scale, but
that link is dissevered, as well as between the keyboard of the modern, and
that of the ancient organ, by the change of scale. The ancient organ was a
Greek instrument, and one of such early date, that it had advanced to the stage
of being fitted with a keyboard, and being played by the fingers (not requiring
the entire hand,) more than a century before the Christian era, as will be
shown hereafter.
It is undoubtedly true that the pitch of musical
instruments has been raised since about 1750. The increase of tension in the
present century has been mainly owing to the improved manufacture of
strings, both in catgut and in wire, but especially to the introduction of
the steel wire of Sheffield, which enables strings to bear greater tension than
the Berlin iron of former days. So it is probable that the A flat of today may
very nearly represent the A of a hundred or more years ago. But although a
pianoforte may sink half a note below the pitch, of the tuning-fork, and will
therefore require to be raised half a note, we do not on that account think it
necessary to alter the names of the keys, or of the notes. No musician would
think of changing the name of Beethoven’s Symphony in C minor, to C flat minor,
or to B minor, because our B might more nearly represent the pitch in Beethoven’s
time. Considering, too, that we have even yet no standard pitch for Europe, and
are not likely to have one until the French will be guided by their men of
science, and slightly modify their present law; also that the only directions
hitherto found among Greek authors are, that every man should tune his lyre by
the lowest audible note of the voice, it will be time to discuss the question
of ancient pitch, when it can be shown that the Greeks had a universal
standard.
Dr. Burney, indeed, offers a speculation about ancient
standard pitch, when he says that a sepulchral urn found in the first
pyramid of Egypt sounded like a bell, adding, if it be true that the Greeks had
their first musical knowledge from Egypt, we may suppose this to be the
standard pitch of the Greeks. To receive such a doctrine will require more
imagination than many possess. For we have first to suppose that a sepulchral
urn was intended to be a musical instrument, and next, to assume that, after
five thousand years, the original weight and density of the metal remain to
assure us of that original pitch. In the meantime, we may be content to
believe in the great probability of variations in pitch in different cities of
Greece, and even in the same city at different times, yet that the modern A
still sufficiently represents the lowest distinctly
audible note of an ancient Greek’s voice, as it does of many voices at the
present time. All that can be known with certainty is, that ancient instruments
must have been tuned alike, when they were to be played together.
The principal difficulties in the path of all students
of Greek music have now been enumerated, but there has always remained one
direct course to learn the Greek system, viz., to go to the fountain head, and
to endeavour to work through, and find the meaning
of, the technicalities, without seeking help from the labours of others in the same field. If they failed, even partially, it would not be
safe to copy from them.
This has been found too time-consuming a course for
able men who desired to know only enough of Greek music to enable them to write
about it. They prudently judged that, when the value of time must be taken into
account, any entirely new history upon so intricate a subject would offer but
the slenderest prospects of a compensating return. That is indeed the main
reason why the world has been allowed to remain uninformed to this day, and it
has been my inducement to take up the subject.
If the present attempt shall be judged to have
succeeded, it will, perhaps, be attributable to the fact, that the study was
undertaken solely for the sake of obtaining better information than
histories of music have hitherto afforded. After having read the published
works of mediaeval authors upon music, and the unpublished contained in the
British Museum, the Bodleian Library, and the Lambeth Library, I next took up
Greek music, as of old a book of chess problems, for the employment of my
leisure time. Only after the Greek problem had been unexpectedly solved, and
the solution had been tested against the difficulties which Boeckh had pointed out in his Metres of Pindar, as well as
against many indicated by others, did the first thought of writing down the
results of reading occur to me. The amusement of investigation was at an end,
and no other terra firma for a new problem
seemed to offer. Desiring a new occupation, it then appeared that my leisure
might be usefully employed in dispelling the mystery that had hung about Greek
music. Moreover, there was a wide field in other branches of history, such as the
debt of the Greeks to Egypt “a different version of the origin of
ecclesiastical tones or scales, and of the kind of notation in which the
Chanting marks for ancient Church services were written” a new account of the
revival period, and to show music in England on four or five lines and spaces
before the time of Guido, to whom much has been attributed, but who was rather
behind than before his age then to explain the only true principles for all music, and to prove
them, so that any one, who only knew the notes, might follow and understand
them. There were also many scraps of information that had not been included in
any history, and which, in the words of Mr. Timbs,
would be “Things not generally known.”
The field was indeed ample, but (writing history not
having been contemplated,) no sufficient provision had been made in the shape
of notes upon former readings, and there was the irksome task of going over the
same ground a second time, under the disadvantages of worn sight, and other
warnings of the advance of time. Hard work was in prospect, for only they who
have tried the experiment can tell the time it may take to find even one
missing link. Still, the main points of history have hitherto been so inadequately
developed, and there has been such copying from untrustworthy writers, as well
as from one historian by another, that any one branch rewritten promised to be
of some use.
CHAPTER II.
ANCIENT SEVEN-STRINGED SCALE.
GREEK music cannot be considered as one of those
subjects of ancient history with which modern science and art have but little
concern, for not only has it been the progenitor of the musical system of
Europe, but even now it is largely adopted, without improvement or change.
It will on that account be convenient to explain it by
the terms of modern art, so soon as identity of meaning shall have been
established, and thus relieve the reader from a mass of ancient technicality.
Such terms, also, as relate to modern practice will be explained pari passu, for, although familiar to
musical readers, it is an object to be even more widely intelligible. Dr.
Burney described Greek music as “a dark and difficult subject” and one that had
“foiled the most learned men of the two or three last centuries”; but no other
difficulties really existed either for him or for them, than in certain words,
and in the ancient technicalities. The music itself is simple in the extreme.
The same comment will apply to Sir John Hawkins’s remark, that “Even at this
day the ablest writers on the subject do not hesitate at saying that the
doctrine of the [Greek] modes is absolutely inscrutable”.
One branch both of the science and of the art, in
which music is still governed by Greek laws, is in the mathematical, and
practical, divisions of notes in the scale. They are precisely the same now as
in the days of the Ptolemies, save in the new-found equal temperament which (introduced for the sake of imperfect instruments) means “putting all
keys equally out of tune”. Whether the strict adherence of the modems to
models of antiquity, as to the formation of the scale, has been for the best,
is one of the questionable cases that will be submitted to the judgment of the
reader hereafter.
The present musical scale is a re-adjustment of the
Pythagorean, by the Greek mathematician, Claudius Ptolemy. The notes are,
therefore, the same at this day (when played in tune) as in the first half of
the second century of the Christian era.
The Greeks had scales beginning upon every semitone of
the Octave, and, therefore, every sharp and flat that we now have.
Every principal Greek scale had what, in modern
technical language, we call its Dominant and Sub-dominant, i.e., the
Fifth and Fourth above the key-note, upon which new scales, connected with the
key, begin. The Greeks expressed those connected scales by the words Hypo or Hypet prefixed to the original name, as:
Dorian, Hypo-Dorian, or Hyper-Dorian. The Hypo scale began a Fourth below the
key-note of the principal scale,(which is the same as a Fifth above it,) and so
answered to our Dominant; and the Hyper began a Fourth above the key-note, and
so exactly like our Sub-dominant.
Here, then, is a complete system resembling our own as
to its keys, as to its familiar modulations, and as to the tuning of its notes.
The music of a Greek maiden accompanying her voice upon the lyre, or other
instrument of the harp kind, nearly two thousand years ago, could hardly be
distinguishable from the minor airs of modern Europe; and the resemblance would
be further strengthened by the Greek maiden’s strict observance of her
key-note, which was quite as strongly enforced by Greek musical laws as by our
own.
There could be but one difference between the two, and
that would hardly be brought into play. The Greeks played and sang in minor
keys only, and their Seventh of the key was the old minor Seventh, or whole
tone below the Octave, in ascending as well as in descending. (In Dr. Burney’s
time, this minor Seventh was called flat Seventh, and the major Seventh,
which is only half a tone below the Octave, was
called a sharp Seventh but, as they do not necessarily fall upon flats or sharps, those
names have been discarded). The minor Seventh was an integral part of the old
minor scale, as the major Seventh is now of the major. An important piece of
history is attached to the old minor, that out of it grew the comparatively
modern major scale, by beginning upon the third note instead of the first.
Thus, beginning on the pianoforte upon C instead of upon A, we change the
ancient key of A minor into the modern C major. A, B, C, D, E, F, G, is the
ancient scale. There could be no such thing as a complete major scale under
Greek laws, because the Seventh was always to be a tone below the key-note.
Many interesting deductions may be made about ancient
music, and these will tend to raise the subject above the technicalities and
the mere history of the art, if the reader will but employ his thoughts to
bring them out. For instance, the character of the music of ancient Egypt and
Babylon may be ascertained by a train of evidence that will leave very little
doubt on the subject; and, by looking at the drawing of an ancient Egyptian
instrument with a long neck, (only supposing the drawing to be an accurate
representation,) he may know, with mathematical certainty, how many notes were,
or could be, played upon every string. The manner of ascertaining it will be
further explained. The present preamble is to prepare the reader to believe
that ancient music has some certainties about it, and is, by no means, the
uninteresting or doubtful study that many might suppose. And now to history.
From the time of the Homeric poems to that of
Terpander, (which is supposed to have been about the middle of the seventh
century before Christ,) the lyre of the Greeks had but four strings. They were
made of sheepgut, which is now technically called catgut.
While the number of strings was limited to four, the lyre must have been used
rather as the substitute for a pitch-pipe to guide in the recitation of epic
poetry, than as a musical instrument. Nothing like tune could be played upon
it, but still there would have been music in the Greek sense of the word, since
there was a combination of recitation, metre, and
rhythm. In the Odyssey we read of a skilled singer and player on the lyre,
(Phorminx), as having changed his chant “to a new string upon a new peg.” That
was the entire musical change, and it was evidently to raise or lower the pitch
of his voice in recitation, to suit a new sentiment in the poem. We may imagine
his chant to have been something like what is now called intoning or monotone.
Monotone practically means only taking a pitch for the voice, for the
articulation of the vowels in speech would alone forbid monotone in a literal
sense, since they of themselves form an ascending or descending scale of
sounds. The custom, that an orator should have a lyre or a pipe by him to
regulate the rise and fall of his voice, endured for many centuries after the
time of Homer.
Greek writers give two different accounts of the
origin of their music; on the one side attributing the discovery of their lyre
to the Greek Hermes, son of Zeus and Maia, daughter of Atlas, and on the other
to the Egyptian Hermes, or Thoth. He was the god of learning, and was commonly
represented by a human figure with the head of an ibis, holding a tablet and a
pen, or a palm branch in his hands. At other times he has a man’s face, with
the crescent of the moon upon his head, supporting a disc. Attention has not
been sufficiently directed to the difference between these two accounts. The
first refers to the primitive Greek system, before the Greeks had learnt
anything of music proper; and the second to their later system, which was real
music, and obviously borrowed from countries of more ancient civilization,
especially from Egypt and Babylon. The first relates to the kind of scale that
is made up by joining one series of four notes, called a tetrachord, to another
series of the same, and making the highest note of the one serve in the double
capacity of lowest note to the other, as B, C, D, E; E, F, G, A. The second account refers to the
embodiment of the tetrachords into the Octave system, as if beginning and
ending on our A.
The story of the former god is told with more detail
in the Hymn to Hermes, (at one time attributed to Homer,) than by Apollodorus,
or other writer. This hymn is obviously of later date than the Iliad or the
Odyssey. It includes the story of Hermes stealing the oxen of Apollo, one of
the fables said to have been invented by Alcaeus of Mitylene.
According to the hymn, Hermes, soon after his birth,
found a mountain tortoise grazing near his grotto, on Mount Kyllene.
He disembowelled it, took its shell, and, out of the
back of the shell, he formed the lyre. He cut two stalks of reed of equal
length, and, boring the shell, he employed them as arms or sides to the lyre.
He stretched the skin of an ox over the shell. It was, perhaps, the inner skin,
to cover the open part, and thus to give it a sort of leather or parchment
front. Then he tied cross-bars of reed to the arms, and attached seven strings
of sheepgut to the cross-bars. After that, he tried
the strings with a plectrum.
This lyre of the Greek Hermes is like some that we see
in ancient sculptures; but the two reeds are generally replaced by two horns,
the curvature of which gives grace to the form.
The idea of these horns seems to have been borrowed
from the Phoenicians, who, according to Herodotus used those of the large
antelope of Libya, and of Egypt (the oryx) for their lyres. The Egyptians did
the same, but sometimes used wood, and had ornamental heads of animals carved
on the arms of their instruments.
The author of the Iliad and of the Odyssey speaks of
the lyre only under its two most ancient names, Phorminx, or Kitharis, but never of its having seven strings. The
Kithara seems to have differed mainly from the Phorminx in being of more
portable size.
The writer of the hymn gives four names to the
instrument, viz., Phorminx, Kitharis, Lyra, and Chelys, (from chelus, the
shell.)
One of the late Greek writers, Manuel Bryennius, bridges over the difficulty of the seven strings
mentioned in the hymn, by asserting that, before Hermes invented the
seven-stringed lyre, men had used one having but four strings. According to Bryennius, the four strings represented the four elements,
earth, water, air, and fire; and Hermes increased the number to seven, to
represent the seven planets.
Mythology apart, we know with tolerable certainty the
date at which the Greeks increased the number of strings on their lyres from
four to seven, because the author of one of the earliest extant treatises on
music, the Introduction to Music, ascribed to Euclid, has preserved for us
two lines from a poem by Terpander, which is as follows :
But we, loving no more the tetrachordal chant,
Will sing aloud new hymns to a seven-toned phorminx.
Terpander here plainly states that the four-stringed
lyre (still called Phorminx) had continued in use up to his own time.
Boethius, while ascribing the invention of the seventh
string to Terpander, supposes the planetary theory to have suggested it to him,
but it is far more probable that the increase was first made, and then the
numerical coincidence with that of the planets, (of the ancients,) suggested
the lyre as a subject for a Greek hymn. This hymn was most likely composed long
after the time of Terpander, when his claim had been forgotten, and after the
Greeks had learnt something of astronomy from Babylon and Egypt. It was then
they began to connect the revolutions of the heavenly bodies with musical
sounds, and astronomy became one of their branches of music.
The arrangement of the seven strings, (the
introduction of which into Greece may be attributed to Terpander,) was to time
them at the same relative distances of tone and semitone as are B, C, D, E, and
E, F, G, A, or as E, F, G, A, and A, B flat, C, D, in the modern scale. Seven
strings sufficed, because the highest string of the lower tetrachord served
also as the lowest string of the upper series. This arrangement of the strings
was called Synaphe, or Conjunction.
Although the Greeks had every kind of Fourth,
or Diatessaron, that we have, yet, in arranging their tetrachords for the
lyre, or for a scale, they chose the one form only, in which the interval of
the semitone is between the lowest note and the next above it. (It may be
necessary to explain to some readers that a musical Fourth consists of two
tones and a half, and a Fifth, of three tones and a half.) The Greek Diapente
had the compass of our Fifth, as the Diatessaron of our Fourth.
Late Greek writers attributed a second and improved
arrangement of the seven strings of the lyre to Terpander, but that improvement
must have been subsequent to the discovery of the Octave system. It has been
attributed, with greater probability, to Pythagoras, who flourished more than a
century after Terpander. The radical change involved in turning tetrachords
into Octaves, shows that the Greeks had at that time begun to learn from other
nations, either by colonization, by trade, or by the visits of musicians. Even
then, such changes are of the slowest growth. In no art or science have changes
been hitherto so slow as in systems of music.
As to the possibility of Terpander’s having also
introduced the second arrangement of the strings, it is very small, considering
his date. He is said to have gained the prize at the first musical contest, at the feast of Apollo Carneius,
in Sparta, BC 676. If so, that victory was gained before Egypt was thrown open
to the Greeks, and at a time when guards were set to prevent the landing of
foreigners by the sea. So, while poetical contest would be an equally
correct translation, it would more accurately describe the nature of his
victory. Philodemus, the Epicurean, who was
cotemporary with Cicero, has distinguished between the music and poetry of the
early Greeks, and based the reputations of Orpheus, Amphion, and the rest, upon
their powers of recitation, and upon their poetry, far more than upon what we
should call their music. If Terpander gained a prize BC 676, it must have been
at least twelve years later before he would have been admitted into Egypt to
learn anything. Egypt was first thrown open to the Greeks by Psammetichus I. Calculated by the Apis Tablets of the Serapeium as the surest guide to
Egyptian dates, the reign of Psammetichus, of
fifty-four years, began in 664, and lasted to 610 BC, and could hardly have
commenced more than a year or two earlier. The probable dates of Terpander and
of his supposed cotemporary, Archilochus, are materially affected by that of Psammetichus, if either of them did all that has been
attributed to them. One of the later myths about Terpander is, that he carried
the lyre of Hermes to Egypt, and taught the Egyptian priests instead of
learning from them. That story was dictated by Greek vanity. Plutarch says
nothing of Terpander’s Carneian victory, but that it
is on record that he gained the prize four times in succession at the Pythian
games for singing to the Kithara, and that he sang his own epic verses as well
as those of Homer. Plutarch further adds that both Olympus and Terpander had
tried a varied style of recitation, but had found it distasteful to, and
strongly opposed by, the Greek public, and had therefore relinquished it. Also,
that Olympus and Terpander limited themselves to one musical mode, or key, and
to three strings, although they well knew how to use a larger number. He
commends them on that account, and says that their chanting far surpassed that
of all others who employed a larger number of strings, and frequent changes of
key, or mode. So the singing by which Terpander gained public prizes was not
his seven-stringed system, but a thoroughly Homeric kind of chanting, like that
commended, in the Odyssey. Some readers may have heard Italian improvisatores, who recite their poems at a
singing pitch of voice, without any tune, not even a chant, in the musical
sense. Their manner of recitation is perhaps something of the Homeric kind. The
Greeks gave the name of rhapsodizing to this manner of reciting epic
poetry. Some, only, of the rhapsodists chanted in musical intervals.
Although Archilochus is often ranked as the
contemporary of Terpander, there was a wide musical step between them, if
Archilochus played his accompaniments on the lyre under the voice-part instead
of in unison with it. According to Glaucus’s Account of Ancient Poets and
Musicians, quoted and approved by Plutarch, Terpander preceded Archilochus, and
upon that theory only is the account of his having played under the voice
probable.
FIRST GREEK TUNING OF THE SEVEN-STRINGED LYRE.
Upper Tetrachord:
d. Nete (shortest string.)
c. Paranete (beside the
shortest.)
b. Paramese (next to
middle,) or Trite (third.)
a. Mese (middle.)
Lower tetrachord :
G. Lichanos (forefinger
string.)
F. Parhypate (beside the
longest.)
E. Hypate (longest string.)
The Greeks had no names of any kind to distinguish
musical notes. They were expressed only by the titles given to the strings of
the lyre, so that the note to be represented by any string would depend upon
the pitch and tuning of the key-note of the lyre. For us it is more convenient
to mark the intervals by the names of modern notes, as above, than to employ
the constant repetition of This was a tone distant, That a semitone.
But that the Greek are names of strings and not of notes, will remove a
long-felt difficulty in the language as to the words Nete and Hypate, which have seemed to vary from their original
senses when applied to music. Although Hypate is
the lowest string in point of pitch and sound, it is the highest in the
Greek sense, which is as to length. Nete, on the contrary, is highest as
to sound, but is lowest when compared in length with any other. It is
upon this ground that Nicomachus tells us that the
gravest, or lowest, sound was ascribed to Saturn from his slow movement, and
being furthest from us; “for”, says he, “Hypate is
the highest”; also, that Nete, the string of quickest movement and
shortest length, producing the highest sound, was ascribed to the Moon, “which
is the lowest of the planets and nearest to the earth.” Again, the longest
string on the lyre was called the first, and the shortest was last. As modern associations are connected with the pitch of
sounds rather than with the length of the strings that produce them, we shall
henceforth speak of Hypate as the lowest
string, meaning that it gives the lowest sound, and of Neteas the highest, meaning that it gives the highest note.
The middle string, or Mese, was the key-note, and
therefore the principal. Nicomachus compares it to
the sun, as being the centre of the musical system,
just as the other is of the planetary. The two were considered to make the
consonance of a Fourth with their extremes on either side; for while the one
passed over two planets, the other passed over two notes, as from a down
to E, or up to d. Nicomachus was a Pythagorean, and the Pythagorean doctrine, derived from Babylon and
Egypt, was that the sun was the centre of the
planets.
If we try this ancient seven-stringed system by a
strictly musical standard, it will indeed be a poor one; but we must take it
for what it was a series of notes arranged for rhapsodizing, before melody, of
the modern kind, was born in Greece. The scale formed by two tetrachords joined
together may have answered for the recitation of an epic poem, and for the
expression of thoughts of an elevated character, but it was unequal to express
the stronger emotions of the mind, such as are called into action by lyric
poetry. The effect of such recitation upon us would be, musically speaking, one
of continued sing-song, because the chant would sound to us as unfinished, and
stopping, rather than ending, upon the third of the key, instead of upon the
key-note. The reason for this is, that we can only associate such a series of
sounds as E, F, G, A, B flat, C, D, with our major scale of F, which includes
the B flat. Near as the Greeks seem to have been to finding out the major scale
when they chose this succession of notes, yet their law that the Seventh of the
scale must be a whole tone (at least) below the Octave, prevented their having,
or at least acknowledging, the major key ever in a perfect form. Many pleasing
melodies have been constructed by the modems within the same compass, by taking
the notes as in a major key, and making F the key-note; but with A
for Mese, and with Greek musical laws, it was impossible to do much. The
two extremes, E and D, were dissonant when sounded together, and the singer, or
reciter, could neither rise a Fifth nor fall a Fifth from the key-note. The
best that could be accomplished with such a scale will be judged by the Greek hymns
in the following pages. In the meantime, we turn to Thoth, the Egyptian Hermes,
and to his lyre.
CHAPTER III
THE following is the popular myth of the
invention of the lyre by the Egyptian Hermes, or Thoth : The Nile, after having
overflowed the whole country of Egypt, when it returned within its natural
bounds, left on the shore a great number of dead animals, of various kinds,
and, among the rest, a tortoise, the flesh of which being dried and wasted by
the sun, nothing was left within the shell but nerves and cartilages, and these
being braced and contracted by desiccation, were rendered sonorous.
Hermes, in walking along the banks of the Nile, happening to strike his foot
against the shell of this tortoise, was so pleased with the sound it produced,
that it suggested to him the first idea of a lyre, which he afterwards
constructed in the form of a tortoise, and strung it with the dried sinews of
dead animals.
Diodorus Siculus says nothing about the Nile, but
that, when the Egyptian Hermes invented the lyre, he gave it three strings, in
allusion to the three seasons of the Egyptian year; for these three strings
producing three different sounds, the acute, the grave, and the mean, the acute
sound answered to summer, the grave to the stormy, or wintry season, and the
mean to spring [and autumn]. The Egyptians made but three divisions of the
year, each of four months; Euripides, says Plutarch, rightly made four
divisions, counting spring and autumn as each of two months, and summer and
winter as each of four months. Any string made of the intestines of animals
will tighten in damp weather, and so give a higher sound than when quite dry.
Egypt had very little rain, but evaporations after floods drew up moisture from
the earth. This association of sounds with seasons was, therefore, a
natural one, and was not confined to Egypt. Plutarch tells us, in his
commentary on Plato’s Timaeus, or, De Animae Procreatione,
that the Chaldeans, or native philosophers of the Babylonian empire, (who,
according to Strabo, had a residence set apart for them in Babylon), connected
sounds with the seasons in the following order: that spring bore the proportion of a Diatessaron,
or musical Fourth, to autumn; that of a Diapente, or Fifth, to winter; and
that of a Diapason, or Octave, to summer. This quotation is useful in
showing that the Chaldeans, or learned Babylonians, had the Diapason, or Octave
system, like the Egyptians. The musical instruments of the people would also
sufficiently prove it.
Boethius, who wrote between five and six centuries
after Diodorus, says that the lyre of Mercury had four strings, the two
extremes being an Octave apart, and the two interior ones sounding the Fourth
and Fifth to the exterior, such as E, A, B, E, in ascending. But the three
strings mentioned by Diodorus suffice to give those intervals, for the
string that is a Fifth from one extreme of the Octave is at the interval of a
Fourth from the other.
And now as to the Egyptian musical instrument which
the Greeks included under the name of lyre. Our learned and accurate
countryman, Sir J. Gardner Wilkinson, says, in his Popular Account of the
Ancient Egyptians, that “Besides harps and lyres, the Egyptians had a sort of
guitar”, (or rather lute,) with three chords, which have been strangely
supposed to correspond with the seasons of the Egyptian year; and here again
Thoth or Mercury has received the credit of the invention; for the instrument
having only three strings, and yet equalling the
power of those of great compass, was considered by the Egyptians worthy of the
god, whose intervention on this and similar occasions is, in feet, only an
allegorical mode of expressing the intellectual gifts communicated from the
Divinity to man.
The guitar consisted of two parts: a long flat neck or handle, and a hollow oval body, either wholly of wood, or covered with parchment, having the upper surface perforated with holes to allow the sound to escape. Over this body, and the whole length of the handle, were stretched three strings of catgut, secured at the upper extremity, either by the same number of pegs, or by passing through an aperture in the handle... The length of the handle was from twice to thrice that of the body; and the whole instrument measured about four feet. ... It was sometimes slung by a band round the neck, like the modern Spanish guitar, to which also it corresponded in being an accompaniment to the voice, though this did not prevent its being part of a band, as the other instruments... The Egyptian guitar may be called a lute.
EGYPTIAN NEFER, OR LUTE.
The second name, lute, is more appropriate, on account of the form of the back and sides of the instrument; because the lute was shaped like the half of a pear cut from the stalk, but the guitar has waving sides, which are at right angles with the front, and a flat back. The following are from Sir J. Gardner Wilkinson’s work :
The Greeks had no musical instruments of any kind with
necks until many ages after the Egyptians had employed them, and, even when
possessing them, they continued to prefer their own, without necks, although
they adopted the system of the Egyptians for the sub-division and measurement
of strings. Yet herein lay the secret, why the ancient Egyptians, Assyrians,
and Babylonians, had learnt the Octave scale system, which is the only true
one, before the Greeks were even a nation.
Every instrument with an open back, like the Greek
lyre, and like a harp without pedals, can yield but one sound from one
string; but if the same string be pressed against a finger-board fixed upon the
neck of the instrument, it mil give a complete scale of sounds. The first
lesson to be acquired from it is, that exactly half of the string will sound
the note that we call the Octave above that which is produced by the whole
length. The only condition is that the string shall be of equal thickness throughout.
Next, that by stopping a quarter of the String, the remainder will sound a
Fourth above the whole; and that by stopping a third part, we obtain the
interval called a Fifth, above the whole.
These three sounds were the foundation of the ancient
Octave scales, and remain the same to this day. The only difference between
ancient and modern science has been in the proportions of the two tones and
semitone, for the filling up of the Fourth. Of these lesser divisions
hereafter.
As the Egyptian lutes had very long finger-boards,
according with the length of the necks, the eye could not, in a moment,
determine accurately the point at which the half, the third, or the fourth part
of a string ended; so they measured off those distances, and tied pieces of
camel-gut round the neck to serve as guides for the finger. Some of the
instruments discovered in the tombs had those divisions remaining. They are
distinctly marked in the painting from which the frontispiece of this volume
has been copied. Technically, they are called frets, from their
fretting, or rubbing, against the strings, when pressed down upon them.
The painting of the Egyptian ladies, who hold these
lutes and the double pipe, is of the 18th dynasty of Egypt. It formed part of
the plastered wall of a tomb at Thebes, and both plaster and painting were
safely brought to England, and subsequently were presented to the British
Museum by Sir Henry Ellis. Some Egyptologists would date them as about the time
of “the king who knew not Joseph”; others, perhaps, at a somewhat earlier
period. If the ladies of Lower Egypt dressed their hair and adorned themselves
in the bewitching style of these charmers of Thebes, we may the more admire the
power of resistance in Joseph. Still, the ladies’ feet are not quite Chinese as
to size. Their lutes are adorned with ivory tail-pieces, and they are pictured
as touching unrepresented strings with a plectrum. Its use was to save their
tender fingers. The plectrum was generally attached to a piece of cord hung
round the neck of the player, but sometimes it was tied to the tail-piece of
the instrument.
Of the two ladies on the right, one is sounding a pair
of pipes, which have ivory mouthpieces, and the other holds a sort of
tambourine, which is neither round nor rectangular. The corners are parallel,
but the sides and ends have an indented curve, to make the form more pleasing
to the eye. There are several examples of this instrument in Sir J. Gardner
Wilkinson’s work. The lady seems to be tapping the tambourine with her fingers
to mark time, but the plaster has unfortunately been broken away at that point,
and the picture is not quite perfect.
The measurements that were necessarily taken for
fixing the frets upon Egyptian lutes, were the obvious due to the discovery of
the relation between sounds and mathematical proportions. The Theorems in
Euclid’s Sections of a String (Sectio Canonis) are
for the purpose of proving the best ways of subdividing strings by measurement
upon a rule placed under them. Then, by calculating the proportions that one
bore to another, to form laws for concord and musical scales. All the science
of Pythagoras was founded upon such proportions.
The Greek names express musical intervals better than
ours. What we call a Fourth they named a Diatessaron (right through four).
A Fourth has but three sounds, unless we include in it the starting note,
instead of, according to the usual calculation, by counting from it. Thus, from
C to F is called a Fourth, but F is only two tones and a semitone distant from
C; for D and E are tones, and from E to F the semitone. So with the Fifth, the
Greek name is Diapente, (through five) but unless the starting note be
included, it consists of but three tones and a semitone, as from C to G.
Aristotle tells us that the Octave was
called Diapason, (through all,) instead of di octo,
(through eight) because, when the Octave was discovered, lyres had only seven
strings. (This is another of many proofs of the true date of the introduction
of the Octave system among the Greeks.) For the same reason, the earliest name
of the Fifth was Dioxia (di' oxeia,
or di' oxeian), meaning through the acute strings of the lyre, because the deficiency of the one string was in the upper
part of the instrument. The Fourth had its fall complement of strings, and was
first called Syllabe, (sullabe), probably
from the lyre-like form of the fingers- upon the four strings; for the lower
four were intended to be played by the thumb and three fingers, and not by the
plectrum, as will be shown later.
The fruits of the elementary knowledge thus acquired
by the Greeks were soon after shown in the improvement of their music. It is
not too much to say that they had not till then any music, in our sense of the
word. Before the reign of Psammetichus I. Egypt had
been a country very little known to the Greeks. No foreigner had been permitted
to settle, or to penetrate into the interior. All were regarded with the same
jealousy that the Chinese exhibit in our own days. But Psammetichus encouraged Greek settlers; gave his own children a Greek education; cultivated
the friendship of the Greek nation, and engaged Ionian and Carian mercenaries
in his army. He also committed Egyptian children to the charge of the
mercenaries, to be taught the Greek language, and so to become interpreters
between the two nations. It is to the ancient civilization, thus first fully
thrown open to the Greeks, that we must attribute the sudden and rapidly-
increased advances they made, within the two or three following centuries, not only
in music, but also in other branches of science and art. The policy of Psammetichus I was followed by his successors, especially
by Amasis, and thirsters after learning of every kind flocked to Egypt, to
become the teachers of their countrymen on their return. Thales and Solon
were among the remarkable early visitors. It was there Thales learnt to divide
the year into 365 days, and to measure the height of pyramids “by the length of
their shadow”, perhaps with the help of an optical instrument for measuring
heights, to which the Greeks gave the name of Dioptra, otherwise we must suppose that the Egyptians taught
our Rule of Three. There Solon copied some of, the best laws for his code.
Pythagoras, who learnt the use of the Dioptra,
is said to have passed twenty or more years in Egypt and Babylon. That he must
have been there, is sufficiently proved by his doctrines. It is also asserted
by Iamblichus, Strabo, and others, supported by Egyptian authority; for
Diodorus Siculus says that the visit of Pythagoras to Egypt was registered by
the Egyptian priests in their books. A tradition is recorded by Strabo that
Plato spent thirteen years of study at Heliopolis. Long after the subjugation
of the country, Egypt remained the great seat of learning for the Greeks. The
Alexandrian library was first formed to collect the wisdom of Egypt.
The fable of Terpander’s having carried the lyre of
Hermes into Egypt is told by Nicomachus. According
to him, Hermes gave his lyre to Orpheus, and instructed him in its use. After
Orpheus had taught Thamyris and Linus, (the latter of
whom taught Hercules and Amphion,) Orpheus, mortally wounded by the women of
Thrace, threw his famous lyre into the sea. Thence it was afterwards discovered
by fishermen, who took it to Terpander, and Terpander took this exquisitely-worked
instrument to the Egyptian priests, and declared himself to have been the
inventor.
We are in no need here of the caution given by
Herodotus, not to trust to Greeks who claimed to have taught the Egyptians,
because, said he, Egypt had copied nothing from Greece. There is a sufficiently
fatal objection to the Terpander lyre-story, in the fact that the Egyptians had
the same musical instrument, and with seventeen strings instead of seven, nine
hundred years before Terpander’s supposed visit; and that they had also a
musical scale of, at least, two Octaves at a still more remote period of
history. The long neck of the Egyptian instrument proves the extent of the
scale. If only one Octave of notes had been required upon one string, a neck,
equal in length to the body of the instrument, would have sufficed; because
half the length of any string of uniform thickness must produce the Octave
above the whole length. But the neck is from two to three times the length of
the body, and that inconvenient extension for the arm can only have been
made for the sake of having two Octaves, or more, upon a string. If the half-length
of a string will produce one Octave, the halving of the remainder must produce
a second Octave above the first. So the especial reason for a neck of evidently
inconvenient length to be reached, was that there might be sufficient length of
string to admit of space between the notes in the higher Octave, for the
fingers to move there with equal freedom. If three-quarters of the entire
length of the sounding part of the string, at that remote period, were made
available for the touch of the fingers upon the neck of the instrument, it was
certainly so made for the purpose of having a scale of two Octaves upon every
string. Lastly, if one of those long-necked instruments had two or three
strings, it was for the purpose of being able to sound two or three notes
together; since the full compass of two Octaves of notes might be had in
succession upon one string.
Nicomachus, quoting Pythagoras and Plato, tells us that the Egyptians ascribed
twenty-eight sounds to the universe, calling it twenty-eight sounding. So the
Egyptians must have had twenty-eight sounds, i.e., twenty-eight notes,
in their scales. That is the precise total number of Greek notes, in their
greater and lesser perfect systems combined, and including all their scales: Diatonic, Chromatic, and Enharmonic. Neither in Egypt
nor in Greece was there an actual limit to twenty-eight sounds, because all
scales were transposable, but only twenty-eight notes could be defined,
starting from any given pitch. Euclid, Nicomachus,
Aristides Quintilianus, and others, enumerate the Greek scales and their
notes, and all authors are agreed as to the number being precisely
twenty-eight. This most remarkable coincidence between Egypt and Greece seems
nevertheless to have escaped the observation of historians of music. If it
stood alone, it would almost suffice to prove the origin of Greek music. The
number is too peculiar to have been arrived at by accident, within a compass of
only two Octaves.
The names of the twenty-eight notes will be given
hereafter in the scales. It may suffice now to say, that in the two-octave
scales there were, as we have, fifteen notes for the Diatonic scale, and that
there were four variable notes for the Chromatic scale, (one in each
tetrachord,) and again four for Enharmonic. Then there was a fifth tetrachord
for the Conjunct or Lesser Perfect System, which added only three notes to the
Diatonic scale, because the lowest note was Mese, belonging to the old series. Add
one variable note for Chromatic and one for Enharmonic in this tetrachord, and
we have twenty-eight in all.
The Greeks were by no means prone to give too much
credit to other nations, yet they did not assert any claim to the Chromatic
scale, which, according to Plutarch, was well known to be of greater antiquity
than the Enharmonic; but Plutarch says that Olympus was the inventor of an
ancient kind of Enharmonic. An analysis of Plutarch’s description proves
that the invention of Olympus consisted in the omission of one string out of
the four in every tetrachord of the already existing Diatonic scale. No use was
made by him of the quarter-tone which distinguished the true Enharmonic.
The scale of Olympus was called by Euclid, and by other writers before
Plutarch, the Common Genus, because those notes were included in all the
genera. Olympus omitted the Fourth and Seventh of the Greek minor scale, and
did nothing more.
The Greeks copied the Egyptians in associating musical
sounds with the heavenly bodies; but, as they made their computations of time
by the lunar month, they connected the twenty-eight notes of the scales with
the twenty-eight days of the moon; and the fifteen notes of the Diatonic scale
were the fifteen days of the moos n’increase. The
Egyptians subdivided the lunar month into weeks through dedicating the first
hour of each of the seven days to the seven planets, as the seven deities, who
were supposed to watch over them. This association seems to have originated in
Babylon. The seven planets and the seven days coincided with the seven notes of
their Octave. If the scale of nature had been followed there would have been
eight sounds in the Octave instead of seven. That is a noteworthy peculiarity,
even in our present system.
One more link between the music of Egypt and of
ancient Greece has been hitherto unobserved, through the misunderstanding of
the musical technicalities in a passage from an early Greek author, and
especially the word anti, which, when taken in the sense
of contra or loco, made the parallel in the context
unintelligible. It is in the treatise on elocution, (Peri Hermeneias),
which has been published under the name of Demetrius Phalereus,
but which Ducange unhesitatingly ascribes to
Dionysius of Halicarnassus. This Dionysius is recorded as a writer on music by
Porphyry.
“In Egypt,” says the author, “the priests hymn the
gods through the seven notes of the scale, sounding them in regular succession;
and, being accompanied by the pipe and by the Kithara, [playing in Octaves] the
resounding of these notes is heard with a very euphonious effect; whereas, he
who omits the accompaniment of a musical instrument with his voice, takes away
nothing less than the due modulation and the fitting tone from the passage”.
This practice of carolling or singing without words, like birds, to the gods, was copied by the Greeks,
who seem to have carolled on four vowels, the
Egyptians having but four. The vowels had probably, in both cases, some recognised meaning attached to them, as substitutes for
certain words of praise, as was the case when the custom was transferred to the
Western Church. The EUOUAE, retained in the Roman Catholic service,
is taken in the sense of Seculorum, Amen, being the
vowels of those words without the consonants. The Eastern Church also had
its NOEANE, NOKANOEANE, ANOAIS, &c. It has been supposed, by
some, that the name of Jehovah, which in Hebrew consists of four letters, IHYH,
originated in this manner of praise.
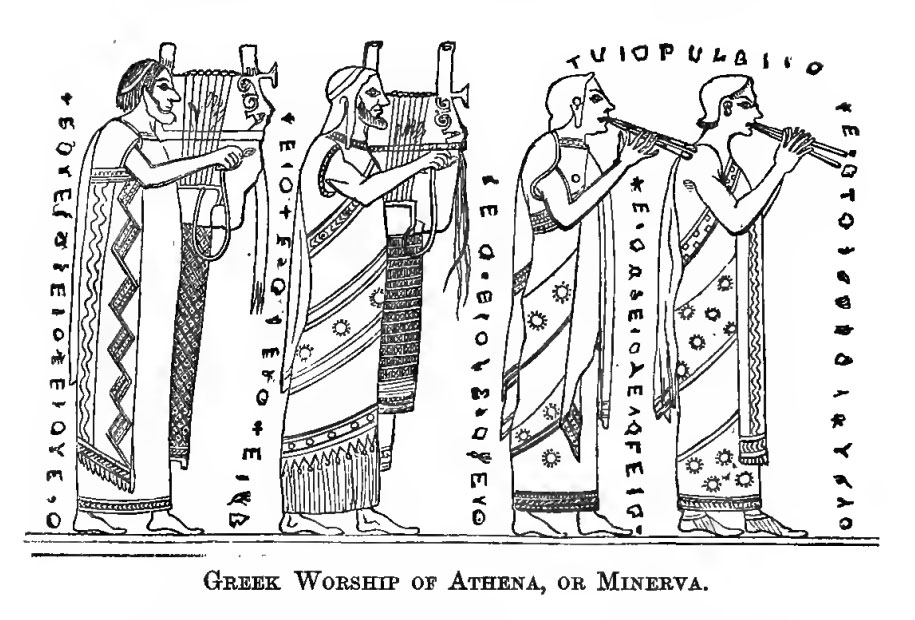
One of the Greek vases in the Museum at Berlin, No.
626, supplies such an exact Greek copy of this Egyptian custom, and so fully
illustrates the preceding quotation, that it is here submitted to the reader.
On the one side is a sacrifice to Athena, or Minerva, and on the other are four
priests, playing on musical instruments, with the inscriptions before them. It
is almost impossible to say with any certainty what all the letters are
intended to be, on account of the carelessness of the execution; but, in the
opinion of the late A. J. Vincent, of the Institut de
France, they are intended for A, E, I, O. The first of the four is very like an
X, and the whole supplies an excellent field for conjecture. It might have been
expected that the Greeks would have sol-faed with
their to, te, ta, te, if
there had been no special reason for another selection.
It should be noted that the lyres in the above have
each seven strings, according to the number of notes employed in this worship,
as described by Dionysius. Next, that the lyres have the double bridge, or Magadis, across the strings, to divide each into two parts,
so as to produce Octaves from the two ends. In ordinary lyres the thumb would
be on the middle string, and the plectrum playing the four nearest to the body,
but that is here reversed. Thirdly, that the priests are playing the higher and
longer ends of the strings with the fingers of the left hand, and the under and
shorter parts with the plectrum (plektron) which each
holds in his right hand. The double pipes are in all probability sounding
Octaves, as with the Egyptians, for the object of double pipes would
necessarily be to produce two simultaneous sounds. The external appearance does
not make one pipe look larger than the other, but the distance of the holes
from the mouth, and the size of the bore of the tube, would determine the
pitch. The pipe on the left of a player was usually to sound the under part,
and had apertures further distant from the mouth.
Gerhard, in his description of the vase, says that the
whole representation is identical with one in the frieze of the Parthenon at
Athens, but that the letters are there scarcely visible.
And now, having shown the Greek copy, we produce the
hitherto unobserved Egyptian Magadis.
The next point is as to an Egyptian tetrachord or four-stringed
arrangement of the notes of a scale. There is in the museum at Florence, said
the late Fr. Jos. Fétis, the lower part of an Egyptian
flute, No. 2688. This is part of a long one, and about three-quarters of a
yard (69 centimetres) long. A Florentine gentleman
took the measurement of all the parts for Fétis, who
engaged a flute-maker of Brussels to reproduce the ancient part in facsimile,
and to add a head piece from designs upon Egyptian monuments. All the minor
details of this experiment may be passed over the one noticeable part is that between the highest
and the lowest note, the interval was a Fourth; and that, as there were five
holes, the pipe must have produced six sounds within this Fourth, or
tetrachord, including the open note of the instrument. That is the precise
number in a Greek tetrachord, when it includes the Enharmonic quarter-tone and
the Chromatic semitone for change into those genera. So that this Egyptian
model appears to have been the one upon which the Greek was formed.
It does not follow that all Egyptian pipes, or all
Greek, were made to include those two peculiar scales, which were comparatively
but little used. Athenaeus says that Pronomus, the
Theban, was the first who played the three kinds of music upon one flute; and
that before him players had separate instruments for each. We may suppose the
same to have been the case with the Egyptians, for we find their pipes or
flutes to have had three, and sometimes four holes, which could only have been
for one or two kinds of scale, where the extreme sounds were but at the
interval of a Fourth.
In addition to many intermediate links with foreign
countries, such as the visits of Asiatics, and of men
from the Isles, to Greece, there were several direct connections between Egypt
and Greece in more ancient times. In 1556 BC, Cecrops is said to have led a
colony from Sais, in Egypt, and to have founded the kingdom of Athens. Neith,
or Net, was the deity of Sais; and her name seems to have led both to the name
of the city and of the Greek goddess, Athena, or Minerva, Plato remarks upon
the asserted identity of the goddess under the Greek and Egyptian names in
his Timaeus. In Egyptian, says Sir J. Gardner Wilkinson, the name was
written from right to left and by adding an A at each end, the Greeks would
make it Athena, reading from left to right. It is well known that the Greeks
adopted the gods of other nations, and their manner of worship, especially
those of Egypt. The Greek vase has already exemplified this in the case of
Athena.
Again, Danaus, who seems to have been a brother of Amunoph III, is also said to have left Egypt and to have
founded Argos, of which he became king, and died, BC 1425. It is probable that
the colonies were formed chiefly by the military class of Egypt, and,
therefore, brought no large amount of learning with them. The higher order of
priests seem to have been too well provided for, to have been easily tempted to
migrate.
There are other links to connect Egypt with Dorians,
Colchians, and others, and much in the mythology, to which space will not
permit me to refer; but one of the strongest proofs to a musical reader is the
identity of a Greek and of an Egyptian song. When Herodotus visited Egypt, he
was struck by nothing more than by hearing what he had thought to be a famous
song of Greek origin, but which he then learnt was a most ancient Egyptian, one a mourning dirge for the premature death of the only
son of Menes, the first king of Upper and Lower Egypt, and that it had been
sung universally in Egypt from time immemorial. The Greek song was a lament for
Linus; and the name of the Egyptian song was a lament for Maneros.
Identity of song argues identity of system of music. There could be no such
identity between a boat-song of the Nile and any European air now. The
tonal systems differ, so that no European can sing or write down the Arab’s
boat-song correctly in our music. There are numerous allusions to ancient
Egyptian music in Greek writers, and a few to Babylonian, but not one among
them has yet been found in which any comment upon difference of systems between
Egypt, Babylon, and Greece, is to be traced. As Herodotus adds that the song of
Linus was sung in Phoenicia, in Cyprus, and elsewhere, though with different
words, we may assume that the identity of musical system extended there also.
Diodorus Siculus says that the musicians and poets of
Greece visited Egypt for the purpose of improvement, and that the Egyptian
priests had records of their visits in their books. The first two names so
recorded were those of Orpheus and Musaeus, and Homer followed. So, at least,
the Egyptians claimed to have taught music and poetry to the Greeks at a very
early period. The later names in Diodorus’s list, such as those of Solon,
Plato, and others, are admittedly authentic.
And lastly, as to the antiquity of the Egyptian Octave
system. Not only have we drawings of the long-necked Egyptian lute in the
eighteenth dynasty of Egypt, but we find it depicted even in the fourth
dynasty, in the reign of Chephren, or Suphis II, second king, sometimes misnamed Sensuphis, who erected the second great pyramid.
Egyptologists differ in estimating these remote dates, so I leave the
reader to select the authority he prefers from the note. It is sufficient to
say that, at the time of the building of the Pyramids, this musical instrument,
which is one of a very advanced kind, was employed as the hieroglyphic for good,
and that the Egyptians were then in such a stage of civilization as to have
other hieroglyphics of the papyrus book, the Egyptian writing materials, and
inkstand, together with sculptures on the largest scale. The paintings of this
long-necked Egyptian lute are sometimes accompanied by the name of the
instrument, but giving only the consonants n f r, and leaving the vowels
to be supplied. Some interpreters have chosen Nofre,
one of the three Coptic dialectal names. Bunsen has a plural termination, Nefru; others Nefr; but,
according to Dr. Birch, Nefer is now the name more generally adopted. The
consonants r and l are interchangeable in Coptic, as in Hebrew,
and hence, perhaps, the Hebrew Nebel, and the Greek Nabla.
The following is the hieroglyphic. The two or four
pegs across the head indicate that the instrument had then, either two or four
strings. As a hieroglyphic, it is more frequently found with one
cross-bar. The second example here given shows the tail-piece to which the
strings were attached, and the bridge over which they passed. The bridge is
represented flat, but must have stood upon its two points. These are copied
from Lepsius’s great work, and are of the fourth dynasty of Egypt.
When the French savants visited Egypt in the
time of Napoleon I., the clue to hieroglyphics had not been discovered, and,
according to them, a lyre of three strings, to represent the constellation
Lyra, was found in a little Egyptian temple, above the great temple of Denderah. It is of
the same kind, says the writer, as Diodorus Siculus speaks of in his History,
of which each string responded to one of the seasons of the year.
The Babylonian and Assyrian sculptures show the Nefer,
as well as the Egyptian, but more sparingly; also the double pipe. In Wilkinson’s Manners
and Customs of the Ancient Egyptians, and in his Popular Account of them
the hieroglyphic will be found, with one bar across the neck of the instrument,
over the doorway of a house, and the interpretation, The Good Abode, or The Good House. Any visitor to the antiquities
of the British Museum will find numerous examples around him, and few will
escape having their attention arrested by the magnificent sarcophagus of
the daughter of Psammetichus II, and of Queen Nitocris, among the inscriptions upon which the
hieroglyphic will be frequently seen.
The preceding painting of four ladies seated, and two
female dancers, is also from Thebes, and of the eighteenth dynasty. Three
hieroglyphic lutes will be found over the head of the third lady, who is
singing and marking time with her hands. The fourth damsel, who is nearest to
the dancers, is playing the tune for them upon two pipes, of the flageolet
kind, and those pipes have ivory mouth-pieces. The painting is upon plaster
that has been safely removed from the wall of a tomb, and is now in the British
Museum.
But a still more curious scene is that of the private
band and the singers of an Egyptian gentleman in the exceedingly early fourth
dynasty. The lute, the papyrus book, and the writing materials are not the only
marvels of that country, so wonderfully civilized, even at the period of the
earliest cotemporary monuments in the world. An engraving, of the same kind as
the following, was taken from the Pyramids of Memphis, and will be found in the
Description de Egypt, published by the French Government. The Memphis band
consists of but one harp, one side-blown flute, together with two pipes, or
flutes, blown at the end, and two conductors beating time. The following is of
Upper Egypt, from the Pyramids of Gizeh. It is copied from Lepsius’s splendid
work, where it is included among other remarkable specimens of the fourth
dynasty.
We have here the private musical establishment,
instrumental and vocal, of an Egyptian gentleman, named Tebhen,
who was master of the tomb. In the large plate of Lepsius he is seated, with
the flagellum in his hand, which is the sign of lordship and
dominion. The upper two rows in the picture exhibit the wealth of the deceased;
but the octavo size of this page admits only the lower two rows, which comprise
his domestic musicians and singers. The hieroglyphics state his distinctions
and his name. For the interpretation of the inscription I am indebted to Dr.
Birch, for no letterpress has yet been published with Lepsius’s Denhmaler. The painting exhibits two harpers with a
conductor; one flute and two pipe players with another conductor; four male
singers, with the right arm extended towards their patron, as if invoking him;
and, behind them, three female singers, who also mark time with their hands.
Lastly, a child, who taps upon some hollow bronze instrument that has an animal’s
head, and which could only be useful for beating time.
This re-duplication of time-keeping, together with the
certain harmony which is being produced from the pipes, prove the advanced and
the rhythmical character of this very early Egyptian music. It is not Homeric
recitation, with license to ramble, but strictly metrical tune. There must have
been a great falling off in the music when it first descended from the
Egyptians to the Greeks, just as a similar decline took place when Greek music,
in its advanced stage, first descended to the Western Church.
The great point to be established by Tebhen’s band is the exceedingly early practice of
instrumental harmony. The flute and pipes cannot be playing in unison, on
account of their varied lengths. Moreover the longest is being sounded in its
lowest notes; but they may be playing the simplest form of harmony in Octaves,
just as the men and women, if singing the same tune together, will make
Octaves. We may indeed conjecture that more advanced harmony must have been
produced from the three pipes, but we have no sufficient proof.
Sir J. Gardner Wilkinson enumerates thirteen different
combinations of instruments that he has noted among the paintings of Egyptian
bands, and he adds that there are many more. Besides these, are singers
accompanied by harp, lyre, lute, by double pipes or flutes, and combinations of
voice, lyre and lute, as well as of solo and chorus without any accompaniment.
Some of the instrumental combinations are of four or five different kinds of
instruments playing together.
The Egyptian flute, which was blown at the side, and
very close to the end, was called the Seba or Sebi. It is
the Photinx and the Plagiaulos of the Greeks, and the Tibia obliqua of the Romans. The Egyptian pipe blown at the end
is the Mam. The precise Greek and Latin names of the last would depend
upon whether that pipe was blown through a reed mouth-piece, or without one. If
it had no reed mouth-piece, being a single pipe, it would be the Monaulos. But I shall describe pipes and flutes more
particularly hereafter.
The harps varied much as to the number of strings. The
upper part of one, in the British Museum, is made for seventeen strings; one in
the Paris collection for twenty-one; and Wilkinson mentions one with
twenty-five pegs, therefore for twenty-five strings. We read of other
harps which had thirty-five, and forty strings; the first, called by the Greeks
the Simikion, and the second, the Epigoneion.
The Egyptian harps that had no poles or pillars to
support the tension of the strings, could only have been tuned for low notes.
Any such tension as that of modem harps would have pulled the frames to pieces.
They had one kind of harp that would have supported much tension, and to that
the Greeks gave the name of Trigon.
We may trace the prototype of every Greek instrument
in Egypt. No kind of advance upon that ancient country seems to have been made
till the three Alexandrian mathematicians, Eratosthenes, Didymus, and Claudius
Ptolemy, appeared successively upon the scene, and improved the scale.
Eratosthenes, the first of them, was born about 276 BC. He was Director of the
Alexandrian Library.
The terra firma of
Egyptian history seems to begin with Menes, the founder of the Empire of Upper
and Lower Egypt. We have a cotemporary monument of
the second dynasty in the Ashmolean Museum at Oxford. It is from the tomb of
King Sent, and we there find a fine specimen of architecture, and the papyrus
roll, or book, is among the hieroglyphics. The Pyramids are the tombs of kings
of the Old Empire, says Bunsen. The royal names discovered in them are all
those of Eratosthenes. The number even of the great Pyramids accords with that
of the kings in Eratosthenes.
According to Diodorus and Plutarch, the shrine at
Memphis contained an inscription commemorating the imprecation of the father of
the unfortunate Bocchoris against the aforesaid
Menes, for having introduced luxurious habits into Egypt, the inconvenience of
which he had felt severely in his Arabian campaign. We know nothing of the
infancy of Egypt. We find it only, from our first point of view, as a country
of high civilization, with writing, with musical instruments of an advanced
kind, and with wonderful architecture. The Lake of Moeris and the Labyrinth are to be numbered among the works of the Old Empire, as well
as the Pyramids. By the list of Eratosthenes, says Bunsen, we obtain a
connected chronology of the Old Empire of 1076 years. The third king of the
13th dynasty lost Memphis and his throne by the irruption of the Shepherds. The
holy city of the Empire [Memphis] was not reconquered and restored till the
18th dynasty. One of its later kings entirely freed the frontiers from the
occupation of the Hyksos.
Egyptian history subdivides itself into three
comprehensive periods: the Old Empire of Menes, (12 dynasties); the Middle Empire, during which Egypt was tributary to
the Hyksos, who reigned in Memphis (13th to 18th dynasty); and the New Empire,
from the 18th dynasty, which expelled the Hyksos, downwards. This threefold
division is established by the monuments, even by those of the 18th dynasty
alone; also by the authority of Manetho. The Hyksos, according to Manetho, were
united North Arabian and South Palestinian races.
The Egyptian laws and religion forbade change and
improvement, while everything around them was changing as the centuries rolled
on. Plato refers to their zealous adherence to antiquity in the following
words: The plan we have been
laying down for the education of youth was known long ago to the Egyptians, that
nothing but beautiful forms and fine music should be permitted to enter into
the assemblies of young people. Having settled what those forms, and what that
music should be, they exhibited them in their temples; nor, was it allowable
for painters, or other imitative artists, to innovate, or invent any forms
different from those which were established, nor was it lawful, either in
painting, statuary, or any branches of music, to make any alteration. Upon
examination, therefore, you will find the pictures and statues made ten
thousand years ago are in no one particular better or worse than what they now
make. (Laws)
The unchangeableness of hieroglyphics has been of the
greatest assistance to modern inquirers; but, as to the ten thousand years,
spoken of by Plato, we must take them cum grano salis, unless we should wish to chronologize the
Egyptian gods.
THE GREEKS4.-Stories about Pythagoras.—The Monochord and the Pandura.—The seven and the eight-stringed lyres.—The difference between a Greek one-octave and a two-octave scale.—Difficulties in classical Greek writers explained.5.-Greek figure of speech "adding a string to the lyre."—Ion's addition of a tetrachord to the earlier system.—The Lesser System Complete.—The Greater System Complete.—Greek Modes and their attributed characters.—Principal modes for the voice.—Fifteen modes.—Harmony of the universe four Octaves and a Sixth.—Pythagorean system of the planets revolving round the sun.—The musical theory.—The doctrine of making the earth a fixed plain in the centre of the universe invented six centuries after the true Egyptian teaching of Pythagoras.6.- singing.—Its high pitch lowered by Claudius Ptolemy.—Greek-written music and plan of tuning the lyre.—Greek Chromatic scale had neither Fourth nor Seventh.—Enharmonic scale.—The scale of Olympus, or Common Genus.—The Chroai, or varied tunings of scales.— The six peculiar scales, called "very ancient" by Aristides Quintillianus7.-Greek Harmony.—Fetis's professed solution.—A passage in Plato re-considered.—Music in Greek education.—Practice of discords mixed with concords—Horace.—Seneca's description of music in an amphitheatre.—Cicero on harmony.—The modern controversy about ancient harmony.8.-Three Greek hymns with music.—Assistance to learning rendered by illustrious Oxonians.—The three hymns the only trustworthy remains of Greek music.—Not duly represented hitherto.—Reasons given.—Now published in modern notation.
|